Notas finas

Alberto Saa

As notas finais estão aqui. O roteiro para solução do exame está aqui. Parabenizo todos os aprovados. Aos que não conseguiram desta vez, ânimo! Estarei sempre a disposição para ajudá-los no que for preciso.

Registro aqui que tenho plena consciência da importância fundamental, para todos, da nota desta disciplina obrigatória, inclusive no que diz respeito a eventual distribuição de bolsas e até desligamento do programa. Eu já fiz todas as revisões de notas possíveis, não é possível fazer nenhum “ajuste” extra, as notas são as definitivas. Porém, se você está absolutamente convencido que houve algum equívoco na correção do exame, escreva-me o quanto antes. Os exames e a P2 estarão disponíveis para entrega a partir da semana do dia 25/7.

Bom recesso.

 

Base de Hamel explícita?

Alberto Saa

O lema de Zorn (e portanto o Axioma da escolha) é invocado para provar que todo espaço vetorial tem um base de Hamel (ver 4.1-7 do livro). Uma pergunta recorrente é: podemos obter uma expressão explícita para uma base de Hamel num dado espaço vetorial? A resposta é não. De fato, tudo (até onde sei) que é obtido via Axioma da escolha não pode ser exibido explicitamente, não são definições construtivas.  Vejam, curiosamente, esta definição informal retirada desse último verbete da wikipedia:

One trivial meaning of “constructive”, used informally by mathematicians, is “provable in ZF set theory without the axiom of choice.”

Nossa discussão dos operadores shift  deu chance para tocarmos nesse assunto para o caso do espaço de Hilbert \ell^2, talvez o mais simples dos nossos espaços de Hilbert de dimensão infinita.  Só para fixarmos notações, um elemento x\in\ell^2 é uma seqüência infinita (x_1,x_2,x_3,\dots) tal que

\sum_{k=1}^\infty x_k^2 < \infty

Sabemos que este espaço é separável e possui uma base de Schauder \{e_k\}, k=1,2,3,\dots já bem conhecida por todos nós. Com esta base, podemos escrever qualquer elemento x\in\ell^2 através da seqüência

x= \lim_{N\to\infty}\sum_{k=1}^N x_k e_k  

sendo o limite entendido a partir da norma usual de \ell^2. O que seria uma base de Hamel para \ell^2? Ora, seria um conjunto de vetores \{\xi_\theta\} LI que nos permitissem escrever, de maneira única, qualquer elemento x\in\ell^2 a partir de uma combinação linear finita (como, a propósito, qualquer coisa que mereça o nome de combinação linear!) de elementos

x =\sum_{k=1}^N \alpha_k \xi_{k}, \quad k\in \{\theta\}

vamos tentar escrever explicitamente quem seria esse conjunto de vetores LI \{\xi_\theta\}. A primeira observação é que podemos escolher este conjunto de modo a acomodar TODOS os vetores usuais \{e_k\}, já que são também LI, e gerarão todos os elementos de \ell^2 que terminam em (\dots,0,0,0,\dots) (os famosos elementos de c_{00}\in\ell^2). Porém, estes vetores não são suficientes para cobrir todo \ell^2 a partir de combinações lineares finitas. Devemos incluir em \{\xi_\theta\} também as seqüências infinitas. Tomemos, por exemplo, esta aqui

\xi_{\theta_1} = \left(1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\dots\right)

que é obviamente LI dos \{e_k\}. Claramente, geramos um subespaço de \ell^2 {\rm span}(\{e_k\},\xi_{\theta_1})\subset\ell^2 bastante grande, mas ainda muito menor que \ell^2. Considere agora esta seqüência

\xi_{\theta_2} = \left(1,-\frac{1}{2},\frac{1}{3},-\frac{1}{4},\frac{1}{5},-\frac{1}{6},\dots\right)

ela não pode ser escrita como combinações lineares das anteriores, i.e., \xi_{\theta_2}\notin{\rm span}(\{e_k\},\xi_{\theta_1}). Podemos, portanto, incluí-la em nossa lista de vetores da base de Hamel, e aumentaremos um pouco o espaço coberto por ela.  Agora, considerem esta seqüência

\xi_{\theta_3} = \left(1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},\frac{1}{5},-\frac{1}{6},\dots\right)

ela também não é combinação lineares das anteriores e, portanto, gera um novo subespaço, e vamos incluía-la na lista. Bem, já está claro um ponto. Quantas seqüências deste tipo temos? Ora, infinitas, com a cardinalidade dos reais! Notem que podemos “contar” estas seqüências da mesma maneira que contamos as seqüencias de 0 e 1 que usamos para, via argumento diagonal de Cantor, provar que \ell^\infty era não separável (1.3-9 do livro).  Já vemos aqui que uma base de Hamel tem cardinalidade alta, i.e., \{\theta\} deve ter a cardinalidade, no mínimo, dos reais para poder acomodar o que fizemos até aqui, em contraste com a base de Schauder, que tem a cardinalidade dos inteiros.

O problema é que o que fizemos até aqui, nem de longe, extingue todas as necessidades para gerarmos \ell^2. Considere, por exemplo, esta seqüência

\xi_{\theta'} = \left(1,\frac{1}{2},\frac{1}{2^2},\frac{1}{2^3},\frac{1}{2^4},\frac{1}{2^5},\dots\right)

Ela não pode ser escrita com combinação linear das anteriores (prove!). Portanto, ela pode ser incluida em nossa lista. Porém, ela dará origem a outras seqüências da mesma maneira que fizemos para \xi_{\theta_1}, e todas serão incluidas na lista. E este processo se repetirá sempre que encontrarmos uma nova seqüência infinita independente das anteriores. Percebe-se que a dificuldade de se construir a base de Hamel é praticamente a mesma de se construir todos os elementos de \ell^2! Uma base deste tipo, em contraste com uma base de Schauder, é muito pouco útil em análises como as que fizemos durante o curso.

Exercício: convença-se que esta construção que estamos fazendo é, na prática, a do item 4.1-7 do livro, a qual está baseada no lema de Zorn.

PS.: Não usamos aqui, em nenhum lugar, o fato de \ell^2 ser um espaço de Hilbert. Poderíamos, por exemplo, usar Gram-Schmidt para ir “ortonormalizando” nossas elementos da base a cada passo, mas isso não é relevante para a nossa discussão. Deem uma olhada neste artigo.

Notas atualizadas

Alberto Saa

As notas atualizadas estão aqui, confiram. A solução da P2 está aqui, e não é um gabarito, é um roteiro que contém inclusive pontos para estudos mais aprofundados. Com relação ao item b da questão 3, optei por dar 0.5 ponto para todos que mostraram que o operador é simétrico. Ganharam o ponto integral os que, além de mostrar a simetria, notaram alguma coisa estranha com o fato do operador ser não limitado.  Qualquer dúvida, escreva o mais rápido possível.

Importante: Os que não obtiveram média 7 entre as duas provas (estão indicados na planilha) devem obrigatoriamente fazer o exame. O conceito final será calculado a partir da média aritmética entre o Exame e a média atual.

Operadores shift, bases de Schauder, de Hamel, etc..

Alberto Saa

Provas são ótimas oportunidades para aprender! Os operadores shift a esquerda e a direita são definidos, por exemplo para seqüências (x_1,x_2,x_3,x_4,\dots) de \ell^2, como

S(x_1,x_2,x_3,x_4,\dots) =(x_2,x_3,x_4,x_5,\dots)\quad\quad (1) 

T(x_1,x_2,x_3,x_4,\dots) =(0,x_1,x_2,x_3,\dots)\quad\quad (2) 

de onde fica bastante evidente o porquê dos nomes destes operadores. O 0 na definição do operador shift a direita T está lá para garantir que T0_s=0_s, sendo neste caso 0_s a seqüência repleta de zeros. Introduzindo-se a base usual de Schauder \{e_k\} de \ell^2, estas duas definições implicam em

Se_{k+1}=e_k, k>1 e Se_1=0,\quad\quad (3)

e Te_k = e_{k+1}, k\ge 1. \quad\quad (4)

Notem que (1) implica em (3), e (2) implica em (4).  Porém, o contrário não é verdade em geral! Isto é o conteúdo da nota de rodapé 1 da solução da prova, um ponto em que o livro é meio desatento.  Tomemos, por exemplo, o caso do operador shift a esquerda S. Suponhamos que ele fosse definido apenas por (3) e pela hipótese de ser linear.  Um elemento v qualquer de \ell^2 pode sempre ser escrito como

v=\sum_{k=1}^\infty \alpha_k e_k,

com todos os alertas pertinentes à interpretação desse limite. Ora, as condições (3) não são suficientes para determinarmos

Sv = S\left(\sum_{k=1}^\infty \alpha_k e_k\right)

Se adicionarmos a (3) e a linearidade a hipótese de S limitado (e portanto, contínuo), podemos escrever

S\left(\lim_{N\to\infty}\sum_{k=1}^N \alpha_k e_k\right) =\lim_{N\to\infty} S\left(\sum_{k=1}^N \alpha_k e_k\right) =\sum_{k=1}^\infty \alpha_k Se_k

e agora utilizando (3) reproduzimos efetivamente (1). O caso do operador shift a direita é análogo. Quer dizer, os operadores shift (1) e (2) são os operadores lineares e limitados tais que (3) e (4) são verificados!

Sem a hipótese de ser limitado, as condições (3) e (4) mais a linearidade não são suficientes para reproduzir (1) e (2). Isto pode ser provado de fato mostrando-se que existem operadores lineares que satisfazem, por exemplo (3), mas que não serão o operador shift a esquerda (1). Pra isso, lançaremos mão de uma base de Hamel para \ell^2.. Relembrando, esta base é um conjunto de elementos \{x_\theta\} de \ell^2 que nos permite escrever qualquer elemento v\in \ell^2 como uma combinação linear única de elementos de \{x_\theta\}

v = \sum_{k=1}^{n} \alpha_k x_{\theta_k}

Uma base de Hamel para \ell^2 deve incluir os elementos \{e_k\}, alem de uma infinidade (não enumerável!) de elementos de comprimento infinito. Basta agora introduzir um operador \cal S linear tal que {\cal S}x_\theta = e_{k} se x_\theta = e_{k+1}, e qualquer outra coisa caso contrário. Teremos assim um operador linear que satisfaz (3), mas jamais reproduzirá (1) e, portanto, não merece o nome de “shift a esquerda”.

Não se preocupem, isto não será cobrado no exame! 🙂

Roteiro para P2 e exame

Alberto Saa

Como disse, cobrimos o capítulo 3 integralmente, e ele será o foco da P2 do dia 30/6. Como também disse, é impossível desvincular o conteúdo deste capítulos dos dois anteriores, então na prática o conteúdo da P2 será os capítulos 1 a 3. (A propósito, com todas nossa discussões sobre funcionais em espaços de Banach após a P1, o capítulo 2 também foi integralmente discutido em sala). Portanto, os exercícios relevantes são todos os dos três primeiros capítulos do Kreyszig.

Do capítulo 4 discutimos várias coisas, algumas em razoável profundidade, como a questão dos espaços reflexivos. Porém, nada específico deste capítulo será cobrado na P2 ou no exame.

Na próxima terça 28/6, falaremos sobre Teorema do ponto fixo de Banach e consideraremos algumas aplicações. É o material contido nas seções 5.1 e 5.2 apenas (5.3 também é relativamente fácil). Este material não será cobrado na P2, mas fará parte, com o conteúdo total dos capítulos 1 a 3, do material do Exame do dia 14/7.

Em caso de dúvidas, escrevam.

Fenômeno de Gibbs

Alberto Saa

Como disse, o fenômeno de Gibbs é a curiosa discrepância que surge nas descontinuidades quando comparamos funções descontínuas e suas séries de Fourier. Relembrando, o que fizemos explicitamente foi mostrar que os conjuntos ortonormais de senos e cossenos eram completos em C[a,b], com o produto interno (e sua norma decorrente) de L^2[a,b] . Porém, como sabemos que C[a,b] é denso em L^2[a,b], temos que os conjuntos ortonormais de senos e cossenos serão também uma base de Shauder para L^2[a,b]. Todas as noções de convergência nesse espaço de Hilbert estão fundamentadas na norma p=2 para as funções, e não na convergência ponto a ponto (p\to \infty), que provavelmente seria a mais “natural” para lidar com funções. Em outras palavras, o fenômenos de Gibbs ocorre porque a norma do L^2[a,b] é insensível a discrepâncias pontuais (na verdade, discrepâncias em qualquer conjunto de medida nula do intervalo [a,b]). Isto ficará mais claro com uma ilustração explícita.

Consideremos a função degrau no intervalo [-\pi,\pi]

f(x) = \left\{\begin{array}{rr} 1, & \quad 0 < x < \pi \\ -1, & \quad -\pi < x <0 \end{array}\right.

Como a função é impar, terá apenas série em senos f(x) = \sum_k b_k\sin kx, sendo

b_k  = \frac{2}{\pi} \int_0^{-\pi} \sin kx \, dx =\frac{2}{k\pi}(1-\cos k\pi)  = \left\{\begin{array}{cl} \frac{4}{k\pi}, & \quad k\ {\rm impar} \\ 0, & \quad k\ {\rm par} \end{array}\right.

Nossa função degrau, portanto, pode ser representada pela série de Fourier

f(x) = \frac{4}{\pi}\sum_{n=0}^\infty \frac{\sin (2n+1)x}{2n+1}

Abaixo vai o gráfico correspondente aos 5 primeiros termos dessa série

Gibbs1

onde já podemos apreciar o fenômeno do “overshooting” na vizinhança da descontinuidade em x=0. Consideremos agora as séries parciais correspondentes à série de Fourier

f_M(x) = \frac{4}{\pi}\sum_{n=0}^M \frac{\sin (2n+1)x}{2n+1}

A figura acima corresponde ao caso M=4. Vamos localizar os pontos críticos de f_M(x) no intervalo (0,\pi), que correspondem aos pontos tais que

f'_M(x) = \frac{4}{\pi}\sum_{n=0}^M {\cos (2n+1)x} = 0 \quad\quad (1)

Notem que

\sum_{n=0}^M {\cos (2n+1)x} =\ {\rm Re}\left(\sum_{n=0}^M  e^{(2n+1)ix} \right) \quad\quad (2)

Desta forma, os zeros de (1) correspondem de fato aos zeros de (2). Ocorre que (2) pode ser facilmente somado, trata-se de uma PG complexa com razão e^{2ix}

\sum_{n=0}^M  e^{(2n+1)ix} = \frac{e^{ix}}{1-e^{2ix}}\left(1 - e^{2(M+1)ix} \right)

Porém, notem que

\frac{e^{ix}}{1-e^{2ix}} = \frac{1}{e^{-ix}-e^{ix}} = -\frac{1}{2i\sin x}

e

 1 - e^{2(M+1)ix} = e^{i(M+1)x}\left(e^{-i(M+1)x} -e^{i(M+1)x}\right) = -2ie^{i(M+1)x} \sin(M+1)x

De onde temos finalmente que

 {\rm Re}\left(\sum_{n=0}^M  e^{(2n+1)ix} \right) = \frac{\sin(M+1)x}{\sin x} {\rm Re}\left(e^{i(M+1)x}\right) = \frac{\sin 2(M+1)x}{2\sin x}

implicando que os zeros de (2) no intervalo (0,1), que serão os pontos críticos de (1) no mesmo intervalo, são os pontos x=\frac{k\pi}{2(M+1)}, com k=1,2,3,\dots. Do gráfico, vemos que o primeiro ponto crítico (k=1) será um máximo localizado em x_* = \frac{\pi}{2(M+1)}. Calculemos agora f_M(x_*)

f_M(x_*) = \frac{4}{\pi}\sum_{n=0}^M \frac{\sin (2n+1)x_*}{2n+1} =\frac{2}{\pi}\sum_{n=0}^M \frac{\pi}{M+1}\frac{\sin \alpha_n}{\alpha_n}

com \alpha_n = \frac{2n+1}{2M+2}\pi. Podemos calcular o limite M\to\infty desta soma se a aproximarmos por uma integral. Notem, primeiramente, que \alpha_0 = \frac{1}{2M+2}\pi, \alpha_M = \frac{2M+1}{2M+2}\pi e que \alpha_{k+1} -\alpha_{k} = \frac{\pi}{M+1}. Em outras palavras, o intervalo (0,\pi) foi dividido em M+1 partes iguais (de fato, os extremos tem metade do tamanho), e estamos somando as áreas de retângulos de largura \frac{\pi}{M+1} e altura \frac{\sin\alpha_n}{\alpha_n}. A figura abaixo ilustra o caso para M=12, sendo que a curva corresponde a função \frac{\sin x}{x}

Gibbs2

Teremos

\lim_{M\to\infty} f_M(x_*) = \frac{2}{\pi}\int_0^{\pi}\frac{\sin x}{x}\, dx \approx 1.179

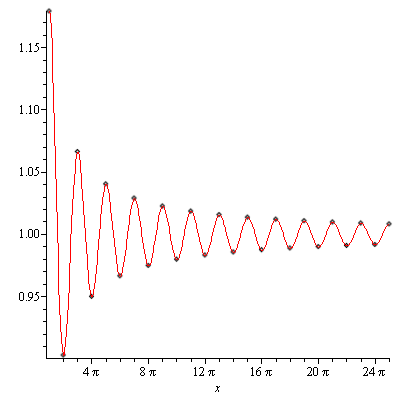
que corresponde ao “overshoot”. Note que no limite M\to\infty, o ponto de máximo x_* está arbitrariamente próximo da descontinuidade x=0.  A figura abaixo ilustra o que ocorre para três valores de M: 4, 16 e 32. Ve-se claramente que o primeiro máximo varia pouco, mas sua localização se aproxima de x=0, de onde percebemos claramente o porquê da norma do L^2[-\pi,\pi] ser insensível a estas diferenças.

Gibbs3

O fenômeno de Gibbs é caracterizado pelo valor relativo do “overshoot”, e não pelo absoluto como fizemos. No nosso caso, a descontinuidade é f(0^+)-f(0^-)=2, então o “overshoot” relativo será

\frac{1.179 -1}{2}\approx 9\%

Que é o famoso resultado. A literatura a respeito é vastíssima. Sugiro este artigo, que é bem contextualizado historicamente e apresenta a derivação original, que não é a apresentada aqui. O resultado original foi deduzido não para a função degrau, mas para uma variação da “dente de serra“. O curioso, e interessantíssimo, é que o fenômeno (incluindo o 9%) é o mesmo para qualquer descontinuidade “razoável”. Isto quer dizer que, do ponto de vista das séries de Fourier, a descontinuidade estudada aqui é genérica. De fato, já discutimos que o ponto fundamental das descontinuidades é o decaimento dos coeficientes b_k. Aqui, como esperado, tratando-se de uma função descontínua, os coeficientes decaem como k^{-1}.

Como disse também, Michelson construiu um “computador analógico” para calcular séries de Fourier, e atribuiu erroneamente o fenômeno de Gibbs a um “defeito” mecânico de seu aparato. Mais informações sobre sua curiosa e engenhosa máquina aqui e aqui. Uma visão “mecânica” de como as componentes de Fourier interagem para gerar a função degrau é dada por esta (ótima!) animação, da wikipedia

 

Fourier_series_square_wave_circles_animation

construida a partir do material apresentado aqui. Notem como os diversos modos de Fourier surgem ao combinarmos  epiciclos.  O video abaixo também é muito interessante.

Um último ponto para mostrar que a convergência pontual (quer dizer, com a norma do L^\infty[-\pi,\pi]) é bastante complicada neste exemplo, surge ao considerarmos não o valor de f(x) no primeiro ponto fixo, mas em todos. Calculemos

f_M\left(x_*^{(k)} \right) =  \frac{2}{\pi}\sum_{n=0}^M \frac{k\pi}{M+1}\frac{\sin \alpha_n^k}{\alpha_n^k}

sendo x_*^{(k)}=\frac{k\pi}{2M+2} e \alpha_n^{(k)} = \frac{2n+1}{2M+2}k\pi. Tomemos o limite M\to \infty, mantendo k constante, de maneira análoga ao que fizemos para o caso k=1 acima

f\left(x_*^{(k)} \right) =  \frac{2}{\pi}\int_0^{k\pi} \frac{\sin x}{x}\, dx

Essa integral é muito bem conhecida. Seu limite para k\to \infty (integral de Dirichlet) é exatamente \frac{\pi}{2}, de onde temos que, longe da singularidade (k grandes), o valor de f\left(x_*^{(k)} \right) tende ao valor esperado f(x)=1. O gráfico abaixo mostra alguns valores de f\left(x_*^{(k)} \right) para k pequenos, de onde vemos que a convergência para o valor  f(x)=1 é o mesmo de uma série alternada.

Gibbs4

No limite M\to\infty, pontos com k finito estão arbitrariamente próximos, sugerindo que a série de Fourier de f(x) é, de fato, complicadamente descontínua na região arbitrariamente próxima a x=0. Contudo, a norma do L^2[-\pi,\pi] é completamente insensível a este rico comportamento  próximo à descontinuidade x=0.

Ainda sobre as funções curiosas

Alberto Saa

Dois últimos pontos sobre nossas “funções curiosas”.

Primeiro, o que ocorreria se tomássemos primeiro o limite m\to\infty em nossa seqüência cujo limite é a função de Dirichlet? Obviamente, a questão se resume a calcular o \lim_{m\to\infty}\cos m!\pi x. Temos duas possibilidades. Se x for racional, sempre existirá um inteiro m tal que m!\pi x seja um múltiplo de \pi. Um resultado mais forte ainda, se x=\frac{p}{q}, m!\pi x será um múltiplo de \pi para todo x tal que q\le m. Disso, temos que, fixando-se um inteiro m, teremos

\cos m!\pi x =1

para todo x=\frac{p}{q}, com q\le m > 3. (Note que \frac{m!}{q} será sempre par para m>3 eq\le m.) Desta maneira, é natural pensarmos que \lim_{m\to\infty}\cos m!\pi x =  1 para x racional. Para x irracional, o limite m\to \infty não existe.

O segundo ponto é uma explicação um pouco mais detalhada sobre a função de Volterra. Como disse, ela está baseada na função f(x) = x^2\sin\left(\frac{1}{x}\right), que é perfeitamente bem comportada na origem, vejam seu gráfico abaixo no intervalo (-0.1,0.1).

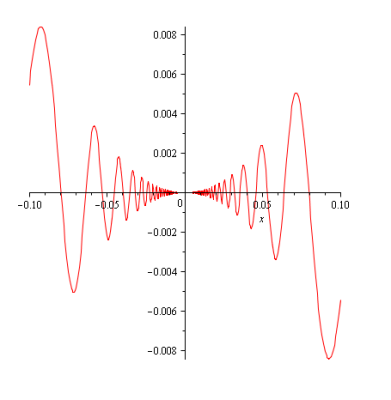
Screenshot from 2016-06-04 16:23:05

Sua derivada é f'(x) = 2x\sin\left(\frac{1}{x}\right) - \cos\left( \frac{1}{x}\right), e seu comportamento na origem é semelhante ao da função que já consideramos aqui. Vejam seu gráfico abaixo, no mesmo intervalo.

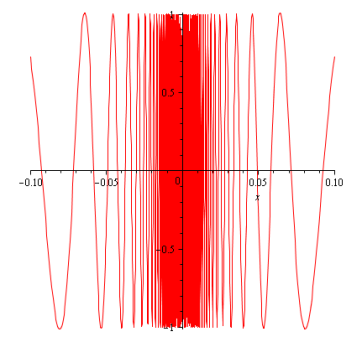
Screenshot from 2016-06-04 16:28:05

A derivada é descontínua no origem, apesar de ser sempre limitada (para intervalos limitados).

Porém, o ponto fundamental na construção da função de Volterra não é a função f(x) (poderia ser outras), mas a maneira como iremos “copia-la” no intervalo em questão, o qual vamos considerar, sem perda de generalidade, como sendo [0,1]. Trata-se de uma construção semelhante ao do conjunto de Cantor, e o conjunto resultante é também chamado de (Smith-)Volterra(-Cantor). A ideia é a seguinte. Começa-se com o intervalo [0,1] e retiramos um intervalo (centralizado) de comprimento \frac{1}{4} (a construção pode ser mais geral, faremos esta por simplicidade). Ficamos agora com dois intervalos disjuntos, exatamente \left[0,\frac{3}{8}\right] \cup\left[\frac{5}{8},1\right]. Repetimos agora o mesmo procedimento para cada um desdes intervalos, porém não retiraremos \frac{1}{4} de seu comprimento (como faríamos na construção do conjunto de Cantor), mas sim \frac{1}{16},  e assim sucessivamente, retirando sempre \frac{1}{2^{2n}} de cada intervalo obtido na n-ésima etapa, veja fig. abaixo (da wikipedia).

Screenshot from 2016-06-04 16:45:30

O conjunto de Volterra é o que sobrará do intervalo original após o procedimento ser repetido infinitas vezes. Corresponde à união dos conjuntos escuros acima. Este conjunto tem inúmeras propriedades interessantes (não é denso em lugar nenhum e não contém nenhum intervalo, dentre outras), mas o que nos importa aqui é que, ao contrário do conjunto de Cantor, sua medida não é nula. É fácil calcularmos o comprimento total das regiões eliminadas (as brancas). Obviamente, o conjunto de Volterra é o complementar. Temos que somar o que retiramos em cada passo do procedimento

\frac{1}{4} + \frac{2}{16} + \frac{4}{32} +\cdots = \frac{1}{2}

Quer dizer, ambas regiões, a branca, que contém intervalos, e a escura (que não contem nenhum intervalo) tem medida total \frac{1}{2}.

A função de Volterra é construida “encaixando-se” nos intervalos brancos uma função construida a partir de  f(x) = x^2\sin x. (Vejam mais detalhes neste artigo). Mostraremos como construir esta função para um intervalo genérico [a,b]. Essa construção deverá ser repetida para TODOS (sim, infinitos) os intervalos brancos. Dividamos o intervalo ao meio e consideremos o pedaço da esquerda, \left[a,\frac{a+b}{2}\right] e tomemos a função

F(x) = (x-a)^2\sin(x-a)

Localizemos agora o máximo de F(x) mais próximo do limite direito do intervalo \left[a,\frac{a+b}{2}\right]. Seja x_m este ponto. Definamos agora a função

H(x) =\left\{\begin{array}{ll} F(x), & a\le x \le x_m, \\ F(x_m), & x_m < x \le \frac{a+b}{2} \end{array}\right.

Agora, reflita esta função H(x) em torno do ponto \frac{a+b}{2}, estendendo-a para todo o intervalo [a,b]. Esta função é, por construção diferenciável em todos os pontos, exceto os limites do intervalo [a,b], vejam sua aparência abaixo. (Retirada do ótimo artigo citado acima).

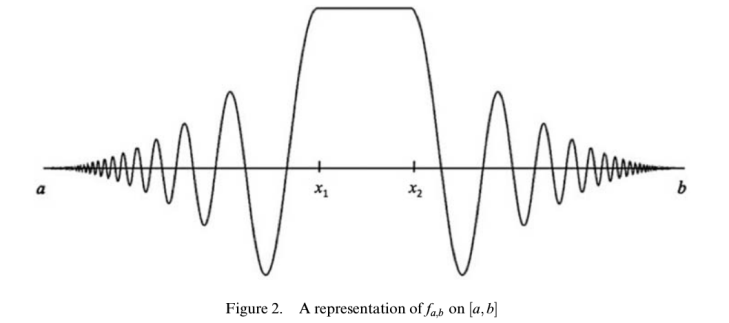
Screenshot from 2016-06-04 17:44:32

É esta função que deve ser “encaixada” em todos os intervalos brancos obtidos acima. Os pontos de descontinuidade das derivadas serão os limites desses intervalos, quer dizer, serão o conjunto de Volterra, que por construção não tem medida nula. Em outras palavras, a derivada da função de Volterra é descontínua em um conjunto de medida não nula e, consequentemente, não tem integral de Riemann.

 

Finalizando com um terceiro ponto nest post que era originalmente de dois, lembrei-me da função pipoca (popcorn function, ou função de Thomae (Tomé)). Ela é definida no intervalo (0,1) como

f(x) = \left\{\begin{array}{ll} \frac{1}{q}, & x {\rm \   racional,\ } x=\frac{p}{q}, \\ 0, & x {\rm \ irracional,}\end{array}\right.

Seu nome curioso vem do seu gráfico (retirado da wikipedia) que lembra pipocas pulando 🙂

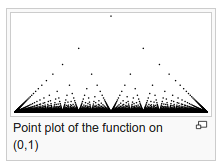
Screenshot from 2016-06-04 16:16:25

A função pipoca é descontínuas nos racionais. (Comparem x=\frac{p}{q}  e  x=\frac{p+1}{q} se q for par!)

As funções de Weierstrass e de Dirichlet

Alberto Saa

Continuando como nossa lista de funções “curiosas”, temos mais duas:

Função de Weierstrass

Esta é um daqueles exemplos que comentei que são definidos a partir da sua série de Fourier. A função de Weierstrass tem as seguintes propriedades curiosas:

  1. É limitada e contínua em todos os pontos
  2. Não é diferenciável em ponto nenhum

Não é difícil construí-la. Vamos considerar funções deste tipo

W(x) = \sum_{n=0}^\infty a^n\cos(b^n\pi x)

com a e b positivos. Com a restrição de b inteiro, temos uma função periódica, mas isto não é necessário aqui. A primeira observação é que para 0<a<1 (o caso a=0 é obviamente trivial) , a função será limitada. Vejamos:

|W(x)| \le\sum_{n=0}^\infty |a^n\cos(b^n\pi x)|  \le\sum_{n=0}^\infty a^n =  \frac{1}{1-a}

para qualquer x\in \mathbb{R}. Há porém um resultado ainda mais forte. Com  0<a<1, essa função será contínua! Vejamos. Vamos considerar as somas parciais

W_m(x) =\sum_{n=0}^m a^n\cos(b^n\pi x)

É claro que W(x) será o limite m\to\infty dessa seqüência de funções. Cada elemento dessa seqüencia é uma função uniformemente contínua, portanto seu limite será também uma função contínua pelo teorema da convergência uniforme. A convergência uniforme permite que calculemos a derivada dessa função como

W'(x) = -\pi\sum_{n=0}^\infty (ab)^n\sin(b^n\pi x)

Se tivermos ab<1, os mesmos argumentos podem ser aplicados, e teríamos uma derivada bem definida. A função de Weierstrass corresponde exatamente à escolha 0<a<1, mas ab>1, para que a derivada não exista! O resultado original de Weierstrass de 1872 mostra que a função para 0<a<1, apesar de ser limitada e contínua, não tem derivada em ponto nenhum se

ab >1 + \frac{3\pi}{2}

Esta condição é suficiente, mas ela pode ser relaxada para ab >1, vejam as demonstrações e um pouco da história aqui ou aqui (melhor. Que sirva de inspiração para que vocês caprichem nas suas dissertações e monografias!). Em geral, a função de Weierstrass tem uma estrutura “fractal”, vejam na ilustração abaixo retirada do artigo correspondente da Wikipedia.

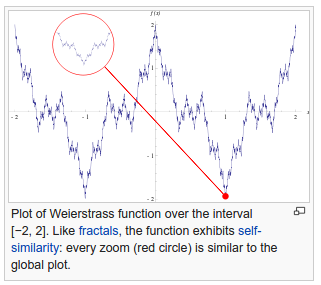
Screenshot from 2016-06-03 15:47:05

Função de Dirichlet

Já comentada em aula, esta função pode ser definida como uma função no intervalo [0,1] tal que

f(x) = \left\{\begin{array}{ll} 0, & x {\rm \ irracional,}\\ 1, & x {\rm \   racional.}\end{array}\right.

É uma função limitada, porém não é contínua em ponto nenhum, e não é Riemann-integrável. O interessante aqui é que esta função pode surgir do limite de seqüências de funções contínuas! Obviamente, neste caso, não podemos ter convergência uniforme, caso contrário f(x) seria necessariamente contínua. Considerem a seqüência de funções

f_{n,m}(x) = \cos^{2n}m!\pi x

com n,m\in \mathbb{N}. Analisemos primeiro o limite n\to\infty. Como o cosseno é limitado em 1, temos duas possibilidades:

\lim_{n\to\infty}f_{n,m}(x) = \left\{\begin{array}{ll} 0, &|\cos m!\pi x| < 1\\ 1, &|\cos m!\pi x| = 1\end{array}\right.

É claro que este limite depende de m!\pi x ser ou não um múltiplo de \pi. Para todo x = \frac{p}{q}, com q\le m, teremos |\cos m!\pi x| = 1. Assim, temos que

\lim_{n\to\infty}f_{n,m}(x) = \left\{\begin{array}{ll} 1, & x=\frac{p}{q}, {\rm\ com\ }q\le m\\ 0, & {\rm caso\ contrario} \end{array}\right.

É fácil agora ver que ao tomarmos o limite m\to\infty, temos a função de Dirichlet.

Função de Volterra e assemelhadas.

Alberto Saa

A função de Volterra é do tipo que precisaríamos para “violar” a definição dos espaços de funções limitadas sem a hipótese de integrabilidade. A função de Volterra tem propriedades curiosíssimas:

  1. É diferenciável (em toda parte)
  2. Tem derivada limitada
  3. Sua derivada não é Riemann-integrável

Esta função é “parente” da função \sin\left( \frac{1}{x}\right), ela é construida a partir de “cópias” da função x^2\sin\left( \frac{1}{x}\right), vejam o verbete da wikipedia acima, ou melhor ainda, este texto.

Um outro exemplo de função limitada que não é Riemann-integrável está aqui.